Radians vs Degrees: Why Two Measures?
- Jonno

- Aug 5, 2024
- 3 min read
Angles can typically be measured in degrees or radians, with each unit offering unique advantages suited to different contexts. Below, I’ll explore each measure, demonstrate the conversion methods between degrees and radians, highlight applications where each is better suited, and explain why both measures exist.
Degrees
A degree is defined by dividing a circle into 360 equal slices (sectors), originating from the centre of the circle. Thus, a full circle encompasses 360 degrees.
The choice of 360 degrees is intriguing for several reasons. Firstly, 360 is the smallest number divisible by every integer from 1 to 6 and 8 to 10. This advantage means that regular polygons with sides fewer than ten (except seven, the ancient ‘perfect number’) can be expressed in whole number degrees. For example, an equilateral triangle has angles of 60 degrees each; if the total degrees of a triangle were, say, 100 instead of 180, dividing its angles into whole numbers wouldn't be possible. This principle applies to polygons with three to ten sides, excluding seven-sided polygons, as noted.
A second reason 360 is notable is that ancient cultures counted 360 days for the Earth's orbit around the Sun, associating each day with a one-degree movement of the Earth along its orbit. Some ancient cultures used a base 60 number system, which fits nicely with 360 degrees. The combination of divisibility and the yearly orbit likely influenced the ancients to ascribe 360 degrees to a circle. Nonetheless, dividing by 360 is somewhat arbitrary. For instance, dividing a circle into 2520 parts would be superior as it includes all integers from 1 to 10 as factors, including 7. However, this would make the unit too small for practical use. Hence, 360 was chosen logically and practically for its user-friendly nature and ease of visualisation in contexts like navigation, construction, and astronomy. It’s convenient for a right angle to have 90 degrees and a straight line to form a 180-degree angle. Therefore, degrees are an accepted (though not derived) SI unit because they are useful in everyday real-world situations.
Radians
One radian is the angle subtended at the centre of a circle by an arc whose length equals the radius of the circle.
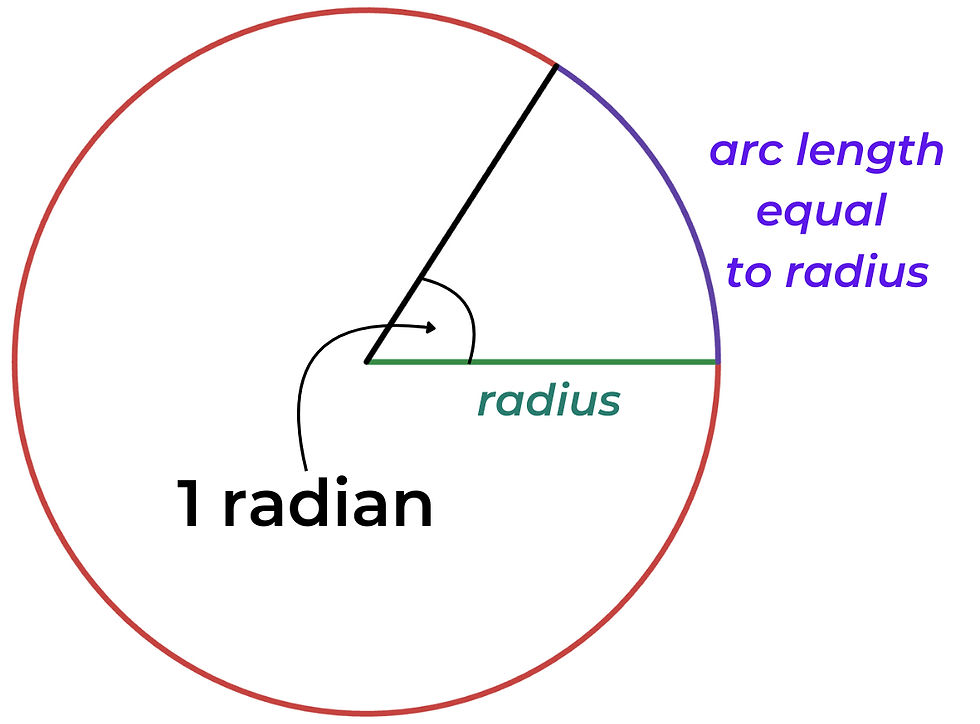
The circumference of a circle with radius r is 2πr. Radians are defined purely by the ratio of arc length to radius, eliminating any arbitrariness and setting them apart from degrees. Consequently, the radian is a derived SI unit. Radians are widely used in higher mathematics and physics, primarily because derivatives of trigonometric functions in degrees include a scaling factor of 180/π , which can be tedious.
Conversion between radians and degrees
π radians = 180 degrees
Convert Degrees To Radians: Multiply by π/180
Convert Radians To Degrees: Multiply by 180/π.
Applications
Degrees and radians are suited to different contexts. Degrees are more intuitive for everyday use and are almost always taught first in school due to their simplicity. While children can easily learn degrees, radians are more challenging due to the introduction of π and their reliance on fractional parts of π. Describing everyday angles in degrees quickly becomes intuitive for students, whereas radians may take months or even a lifetime to grasp fully. However, radians are best for calculating arc lengths and areas of sectors. In physics, radians are better for solving problems such as angular speed or objects moving in a circular path. As mentioned, radians are also preferred in calculus to eliminate the scaling factor introduced by degrees.
Conclusion
Whether calculating the angle of a ramp in degrees or solving calculus integrals in radians, both units have their place in mathematics. Degrees are best for everyday use and are more easily grasped by younger students. Radians are better for calculus and physics. In short, without radians, many calculations in physics and mathematics would be inefficient and tedious. Without degrees, working with angles in everyday life would be unnecessarily complicated. Thus, having both measures is beneficial.




Commentaires